LCS - 최장 공통 부분 수열

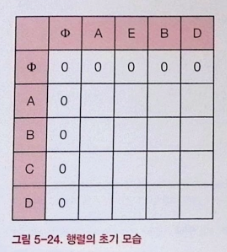
• 두 문자열 $X,Y$의 최장 공통 부분 수열
  • $X$의 부분 수열 이면서, $Y$의 부분 수열은 공통 부분 수열(Common subsequence)

재귀(하향식)

• 앞/뒤 글자 비교 (인덱스 or 글자 자체로 비교)
  • 맨 앞/맨 뒤 둘다 가능
    • 둘 중 한 방향을 정하고 비교
• 점화식
  • 같으면 앞 글자 제외하고 재귀 호출
    • LCS('ABCD', 'AEBD') = 1 + LCS('BCD', 'EBD')
    • 같으니 +1 bias
  • 다르면 각 $X,Y$에서 앞 글자가 없는 경우의 최대
    • LCS('ABCD', 'AEBD') = MAX(LCS('BCD', 'AEBD'), LCS('ABCD', 'EBD'))
• 메모이제이션
  • LCSLTable[m][n]
  • [m][n]이 두 문자열의 최장 공통 부분 수열 길이

•   #include <bits/stdc++.h>
    using namespace std;
    
    int LCS(string& a, string& b, int i, int j, vector<vector<int>>& dp) {
    	if (i == a.size() || j == b.size()) return 0;
    	
    	int& ret = dp[i][j];
    	if (ret != -1) return ret; // 캐싱 - 이미 계산된 값이면 바로 반환
    
    	if (a[i] == b[j])
    		ret = 1 + LCS(a, b, i + 1, j + 1, dp);
    	else
    		ret = max(LCS(a, b, i + 1, j, dp),
    				  LCS(a, b, i, j + 1, dp));
    
    	return ret;
    }
    
    int main() {	
    	string a, b;
    	cin >> a >> b;
    
    	vector<vector<int>> dp(a.size(), vector<int>(b.size(), -1));
    	cout << LCS(a, b, 0, 0, dp) << "\n";
    }

상향식

• 상향식으로 캐시 테이블
• 2차원 DP
  • 행 - $X$
  • 열 - $Y$
• 초기 값
  • 
• 글자가 같으면
  • 좌상 대각선 값 + 1
    • 재귀에서 앞에서 부터 비교하면서 +1 bias가 추가되는 부분이 결론적으로 각각 글자를 1칸 씩 뛰어넘음으로 대각선으로 가는 것
• 다르면
  • MAX(위쪽 셀값, 왼쪽 셀값)
    • 재귀에서 글자가 다른 경우, 각 글자의 앞 글자가 없는 2경우의 최대값을 가져옴으로
• 
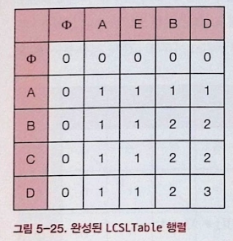
• 최장 공통 부분 수열 출력
  • 완성된 DP 테이블에서 역순으로 순회
  • 대각선 이동시 LCS 추가된다
  • 같으면 포함
  • 다르면 왼쪽, 위쪽 셀 값중 큰 곳으로 이동
• 다이내믹 프로그래밍 완전 정복 p.158